Sistemas de medida de ángulos: RADIANES

Un radián es la unidad de medida de un ángulo con vértice en el centro de una circunferencia y cuyos lados delimitan un arco de circunferencia que tiene la misma longitud que el radio. El radian (rad) es la unidad de medida para ángulos en el Sistema Internacional de Unidades (S.I.).

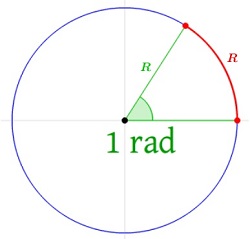
Un RADIÁN es el ángulo que aparece cuando la longitud del arco de la circunferencia, mide lo mismo que el radio. El radián no depende del del tamaño de la circunferencia, ya que recuerden que en el tema pasado se establecio que la circunferencia tiene una longitud de 360°, con esto se puede resumir que;  un radian equivale al ángulo central que abarca un arco de longitud igual al radio.

Bien, ya que sabemos qué es un radián vamos a relacionarlo con la otra unidad de medida de ángulos que conocemos: el grado sexagesimal (o simplemente grado). La equivalencia entre estas dos medidas es la siguiente:

180°= π rad

Por tanto, un radian corresponde a, aproximadamente, 57.295°

EQUIVALENCIA DE RADIANES Y GRADOS SEXAGESIMALES

Antes de pasar a la equivalencia entre los dos sistemas mas usados para medir ángulos, hay que recordar que es el Sistema sexagesimal: Es un sistema de numeración en base 60. Es un sistema que se usa para medida de ángulos y de tiempo. En el sistema internacional de medidas la unidad de ángulo es el radián y la unidad de tiempo es el segundo.

Medida de ángulos:  1° (grado) = 60’ (minutos); 1’ (minuto) = 60” (segundos).

Para comprender el concepto de un grado sexagesimal se parte de que un ángulo recto mide 90
grados sexagesimales. Si el ángulo recto se divide en 90 partes iguales, cada parte tiene una medida
de un grado sexagesimal.

Ya hemos estado trabajando con este sistema, puesto que lo utilizamos en los temas pasado par amedir e incluso clasificar ángulos y triángulos. Pero ahora, empezaremos a realizar la equivalencia del sistema sexagesimal al sistema cíclico, es decir: de GRADOS A RADIANES.

La expresión general que permite relacionar las medidas de un ángulo expresadas en grados y radianes es la siguiente:

G	=	R
360º		2 · π

Donde,

G   es la medida del ángulo expresada en grados sexagesimales (º)

R   es la medida del ángulo expresada en radianes (rad)

Si lo que se desea es calcular los grados sexagesimales a partir de radianes, se despeja G de la expresión anterior, quedando:

	R
G  =		· 360º
	2·π

-  EJEMPLO 1:  Pasar 1 radián a grados sexagesimales

Sustituyendo el valor de 1 radián en la expresión anterior resulta:

	1
G  =		· 360º  =  57,29578º
	2·π

Por tanto, 1 rad = 57,29578º

-  EJEMPLO 2:  Pasar π/4 radianes a grados sexagesimales

Sustituyendo π/4 en la expresión anterior se obtiene:

	π/4
G  =		· 360º  =  45º
	2·π

Por tanto, π/4 rad = 45º

VÍDEOS EXPLICANDO LA EQUIVALENCIA:

BLOQUE II.- ÁNGULOS EN LA CIRCUNFERENCIA.

Después de ver las posiciones relativas de dos circunferencias, hoy vamos a estudiar los ángulos de una circunferencia.

En la enseñanza de la Geometría se comprenden de forma fragmentada los conceptos y teoremas, y su utilización en la resolución de problemas es muy limitada. La Geometría está encaminada a prepararse para resolver problemas geométricos de construcción, de cálculo y de demostración a partir de las relaciones de igualdad de triángulos, en la circunferencia y la semejanza.

El tratamiento de estos conceptos en la solución de problemas de este tipo, posibilita la formación de una visión global inicial de las habilidades matemáticas para calcular longitudes de segmentos, arcos y amplitudes de ángulos en situaciones dadas.

Los ángulos que intervienen en una circunferencia es el punto de unión entre las figuras geométricas y el circulo, recordando que los triángulos (figura central de la geometría) contiene dos puntos centrales que implican una circunferencia, ahora bien se pueden podemos clasificarlos en 5, los cuales tienen características propias y formula para calcular su arco o bien su angulo, que están relacionados, y estos ángulos son los siguientes:

Ángulo central: Es el ángulo que tiene su vértice en el centro de la circunferencia, es decir, un ángulo determinado por dos semirrectas que tienen el origen en el centro, y por tanto son radios de la circunferencia. Los puntos correspondientes al círculo abarcados por el ángulo central se llaman sector circular correspondiente a dicho ángulo.
Diremos que dos ángulos son equivalentes cuando sus ángulos centrales correspondientes sean iguales.



Característica:    La medida del arco AB es la del ángulo central AOB.
Arco AB = Angulo AOB


Ángulo inscrito: Es el ángulo cuyo vértice se encuentra en un punto cualquiera de la circunferencia. Además los lados de un ángulo inscrito son secantes a la circunferencia. El valor del ángulo central es la mitad del ángulo inscrito que abarca el mismo arco.
Si el ángulo central es un ángulo de 180º, entonces el ángulo inscrito es un ángulo de 90º, es decir, un ángulo recto.




Característica: El ángulo inscrito mide la mitad que el arco que comprende.


Ángulo semiinscrito: Es el ángulo cuyo vértice es un punto de la circunferencia y uno de sus lados es tangente a la circunferencia mientras que el otro es secante a ella. El valor de un ángulo semiinscrito es igual al del ángulo inscrito que abarca.



Característica:  vale la mitad que el ángulo del centro.


Ángulo exterior: Es el ángulo que tiene su vértice fuera de la circunferencia, es decir que la distancia del vértice al centro es mayor que el radio de la circunferencia; y sus lados son secantes a la circunferencia. El valor de un ángulo exterior es la semidiferencia de los arcos que abarca.



Caracteristica: La medida del ángulo exterior es la semidiferencia de los arcos que abarca.

Ángulo interior: Es el ángulo cuyo vértice está en la parte interior de la circunferencia, es decir, que la distancia del vértice al centro de la circunferencia es menor que el radio. El valor de un ángulo interior es igual a la semisuma de los ángulos que comprenden él mismo y su opuesto.




Característica; La medida del ángulo interior es la semisuma de los arcos que comprenden él y su opuesto.


En esta parte te presentaremos algunos ejercicios:


1.- Calcular : “x”


Respuesta: 70, ya que el angulo inscrito es la mitad de un angulo central.

Ahora: ANALIZAR LOS VÍDEOS EN DONDE SE EXPLICA COMO CALCULAR LA APRTURA DEL ANGULO, PERO QUE ES IMPORTANTE PODER IDENTIFICAR DE QUE ANGULO SE TRATA.

BLOQUE II.- POSICIÓN RELATIVA DE DOS CIRCUNFERENCIAS

La posición relativa entre dos circunferencias viene determinada por la distancia entre sus centros (d) y el valor de sus radios R y R'. Se tienen los casos siguientes: Exteriores: La distancia entre los centros, d, es mayor que la suma de los radios. Las circunferencias no tienen puntos en común. Tangentes exteriores: La distancia entre los centros es igual a la suma de los radios. El centro de cada circunferencia es exterior a la otra y tienen un punto en común, punto de tangencia. Secantes: Tienen dos puntos en común. La distancia entre sus centros es menor que la suma de sus radios y mayor que su diferencia. Tangentes interiores: Tienen un punto en común y la distancia entre sus centros es igual que la diferencia de sus radios.  Interiores: No tienen ningún punto en común y la distancia entre sus centros es menor que la diferencia de sus radios. Interiores concéntricas: No tienen puntos en común y la distancia entre sus centros es cero (coinciden). Ahora, comparto video en donde se explica de forma visual.

BLOQUE II: ELEMENTOS DE LA CIRCUNFERENCIA

De manera formal, una circunferencia se define como el lugar geométrico de los puntos del plano equidistantes de otro, llamado centro de la circunferencia.

No debemos nunca confundir el concepto de círculo con el concepto de circunferencia, que en realidad una circunferencia es la curva que encierra a un círculo (la circunferencia es una curva, el círculo una superficie, (SE COMENTO EN CLASE: ÁREA Y PERÍMETRO).

También se puede definir como el lugar geométrico de los puntos del plano que están a la misma distancia de un punto fijo, llamado centro.

A continuación vemos una imagen de una circunferencia.

En realidad, y de manera más sencilla, una circunferencia es el conjunto de puntos situados en el plano todos a la misma distancia de un mismo punto central, al que llamaremos centro.

Los elementos mas importantes de la circunferencia son los siguientes:

• Centro.

• Diámetro

• Radio

• Cuerda

• Secante

• Tangente

• Arco

El circulo es la porción de plano limitada por una circunferencia. Dentro de el se puede distinguir diferentes figuras, que sin porciones de un circulo, los cuales se pueden nombrar como:

• Segmento circular

• Sector circular

• Semicírculo

• Corona circular

• Trapecio circular.

Bloque I. Parte 3

El teorema de Pitágoras

Objetivos de aprendizaje

·         Usar el Teorema de Pitágoras para encontrar el lado desconocido de un triángulo rectángulo.

·         Resolver problemas de aplicación con el Teorema de Pitágoras

Introducción

Hace mucho tiempo, un matemático Griego llamado Pitágoras descubrió una propiedad interesante de los triángulos rectángulos: la suma de los cuadrados de las longitudes de los catetos es igual al cuadrado de la longitud de la hipotenusa del triángulo. A esta propiedad — que tiene muchas aplicaciones en la ciencia, el arte, la ingeniería y la arquitectura — se le conoce como Teorema de Pitágoras.

Echemos un vistazo a cómo este teorema puede ayudarnos a saber más sobre la construcción de los triángulos. Y la mejor parte — ni siquiera necesitas hablar Griego para aplicar el descubrimiento de Pitágoras

El teorema de Pitágoras

Antes de hablar de la definición del teorema de Pitágoras, debemos recordar dos ideas básicas de la matemática y específicamente de la geometría:

1. La definición de un triángulo rectángulo; en palabras simples, un triángulo rectángulo es aquel triángulo que tiene 90° por medida en uno de sus tres ángulos internos.
2. Los lados en un triángulo rectángulo tienen nombres, de esta forma llamamos hipotenusa al lado de mayor tamaño que además es el que siempre se encuentra en el lado opuesto al ángulo interno que es el que tiene 90° como medida, los otros dos lados reciben la denominación de catetos y la intersección de ambos se lleva a cabo en el ángulo rectángulo interno característico de todo triángulo rectángulo.

Luego de recordar estas dos premisas básicas de la teoría de triángulos, estamos en capacidad de analizar la pregunta ¿qué es el teorema de Pitágoras?

El teorema de Pitágoras es una propuesta matemática que se puede demostrar de distintas maneras; este teorema indica la relación existente entre los catetos y la hipotenusa de un triángulo rectángulo en donde si elevamos al cuadrado cada uno de los dos catetos y sumamos ambos, tendremos una medida igual al cuadrado de la hipotenusa.

Es decir, si llamamos a la hipotenusa h y a cada uno de los catetos a y b, tendremos:


a^2 + b^2 = h^2

Las aplicaciones del teorema de Pitágoras son muchas y vienen ayudando a las distintas civilizaciones desde su descubrimiento realizado por Pitágoras de Samos hace ya bastantes siglos, incluso antes de la era Cristiana. Lo fácil que resulta aprender esta fórmula matemática hace que se pueda enseñar desde los años básicos de educación en donde el conocimiento y aplicación de la fórmula del teorema de Pitágoras se afianza y se desarrolla principalmente en las aulas de clase con el paso de los años.

Demostración geométrica del teorema de Pitágoras

Partimos del triángulo rectángulo genérico representado anteriormente para enunciar el teorema. Entonces, construimos un cuadrado cuyo lado mida la suma de los catetos, es decir, un cuadrado de lado . Estaremos de acuerdo que el área de este cuadrado es .

Hemos puesto las medidas de  y  de tal forma que si trazamos las hipotenusas construimos cuatro triángulos rectángulos como el genérico, quedando un cuadrado interno de lado .

Ahora podemos escribir el área del cuadrado grande, que antes hemos calculado como  (b+c)², pero haciendo la suma de las áreas de los cuatro triángulos más el cuadrado interno.

Tenemos cuatro triángulos rectángulos de área  At= b*c / 2 y un cuadrado de área  a² . Nos queda pues la siguiente igualdad:

Desarrollamos a los dos lados

Con lo que acabamos de obtener la relación que enuncia el teorema de Pitágoras.

Encontrando la longitud de la hipotenusa

Puedes usar el Teorema de Pitágoras para encontrar la longitud de la hipotenusa de un triángulo rectángulo si conoces la longitud de los otros dos lados del triángulo, llamados catetos. Puesto de otra manera, si conoces las longitudes de a y b, puedes encontrar c.

En el triángulo anterior, tenemos las medidas de los catetos a y b: 5 y 12, respectivamente. Puedes usar el Teorema de Pitágoras para encontrar el valor de la longitud de c, la hipotenusa.

Usando la fórmula, puedes encontrar que la longitud de c, la hipotenusa, es 13. 

A continuación se presenta un vídeo de como se aplica el Teorema de Pitagoras en una serie de ejercicios:

Ejemplos de la aplicación del Teorema en la vida cotidiana:

Descargar ejercicios que se trabajaran durante clase, además de una autoevalución que se implementara:

https://drive.google.com/open?id=1Vrj6t849BaYKWNasCiBzCPEwZw0UWVdy

https://drive.google.com/open?id=1tIMKPX5bUPS4C_tnpm7kKsAscegoUBus

BOQUE I. parte 2

Triángulos.

El triángulo es un polígono de tres lados que da origen a tres vértices y tres ángulos internos. Es la figura más simple, después de la recta en la geometría. Como norma general un triángulo se representa con tres letras mayúsculas de los vértices (ABC).

De acuerdo a la longitud de sus lados, un triángulo pude clasificarse en equilátero, donde los tres lados del triángulo son iguales; en isósceles, el triángulo tiene dos lados iguales y uno desigual, y en escaleno, donde el triángulo tiene los tres lados desiguales.

También se pueden clasificar según la medida de sus ángulos, puede ser un acutángulo, donde los tres ángulos son agudos; es decir, ángulos menores que 90°. Si un triángulo presenta un ángulo recto o ángulo de 90° se dice que es rectángulo, y si presenta a uno de los tres ángulos como obtuso; es decir, un ángulo mayor que 90° se considera como obtusángulo.

Características y propiedades de los triángulos:

1. Un lado de un triángulo es siempre menor a la suma de los otros dos lados (a < b + c), pero mayor que su diferencia (a > b - c).
2.  La suma de todos los ángulos interiores de un triángulo da siempre 180º (A + B + C = 180º).
3. El ángulo exterior de un triángulo es iguales a la suma de los ángulos interiores no adyacentes (a = A + B).
4. A mayor lado en un triángulo se opone también mayor ángulo.
5. En un triángulo con los lados iguales, sus ángulos opuestos son también iguales.
6.  La suma de todos los ángulos exteriores es de 360°.

para la clasificación de triangulo se determinan de acuerdo a dos características, por sus lados y por la apertura de sus ángulos.

El triángulo según sus lados:

• Triángulo equilátero. Los triángulos equiláteros tienen tres ángulos iguales en longitud. También miden lo mismo sus ángulos siendo los interiores de 60º.
• Triángulo isósceles. Los triángulos isósceles son aquellos con dos lados y dos ángulos iguales.
• Triángulo escaleno. Los triángulos escalenos son aquellos que no tienen ningún ángulo o lado igual.

El triángulo según sus ángulos

• Triangulo rectángulo. Los triángulos rectángulos son aquellos con un ángulo interior recto (90º). Este ángulo se delimita por dos lados llamados catetos. El lado de mayor longitud es la hipotenusa.
• Triángulo acutángulo. Los triángulos acutángulos con aquellos con tres ángulos interiores agudos (menor de 90º).
• Triángulo obtusángulo. Los triángulos obtusángulos son aquellos con un ángulo obtuso (mayor de 90º).

A continuación se presenta el link de la presentación, en donde ademas de lo anterior se explica las alturas y centros del triangulo, así como el tratado de similitud y congruencia.

https://drive.google.com/open?id=1RhWYYs87NUSE6nP8Vd6doB0x6Y1yKyMI

ACTIVIDAD: descargar documento y trabajarlo en clase.

https://drive.google.com/open?id=14mqGijcWaU00yi8IJE3xC9eEKr9_rUXE

Link para descargar imagen:
https://drive.google.com/open?id=1UEkMBna8WNGE_8HyDcw1n_OGSuSSjAM3

BLOQUE I: parte 1

ÁNGULOS.

Del griego  agkulos, encorvado, doblado.

Se denomina angulo a la abertura entre dos lineas rectas llamadas lados del ángulo que se interceptan en un punto llamado vértice.

El sistema que se utiliza para medir y dibujar ángulos se llama sistema sexagesimal. dicho sistema utiliza al grado ( ° ) como unidad de medición. También utiliza submúltiplos que lo hacen mas exacto. Sus subunidades son el minuto ( ' ) y el segundo ( " ), que:

1° = 60'

1' = 60 "

Para el estudio del angulo se clasifican por medios de tres aspectos: medida, posición y suma.

Clasificación por medida:

• Agudo.
• Recto.
• Obtuso.
• Llano.
• Cóncavos.
• Nulo  o completo.

Clasificación por posición:

• consecutivos.
• adyacentes.
• opuestos por el vértice.

Clasificación por suma:

• Complementarios.
• Suplementarios.

Y como caso especial, se tienen a los ángulos formados por dos lineas paralelas cortadas por una transversal,  que se clasifican en:

•  Alternos internos.
• Alternos externos.
• Correspondientes.
• Colaterales o conjugados.

A continuación se presenta el link para descargar presentación en formato PPT, que se expuso en clase, en donde se define cada uno de los anteriores.

https://drive.google.com/open?id=1Mt1o_QjNyhrGngaX7pyvTg26sSD7Dkxw

ACTIVIDAD:

Descargar documento de ejercicio 1, que se trabajara durante clase.

https://drive.google.com/open?id=1JhmkDGcHalFNHwov_yvgvCYi9S79sMQA