En la enseñanza de la Geometría se comprenden de forma fragmentada los conceptos y teoremas, y su utilización en la resolución de problemas es muy limitada. La Geometría está encaminada a prepararse para resolver problemas geométricos de construcción, de cálculo y de demostración a partir de las relaciones de igualdad de triángulos, en la circunferencia y la semejanza.
El tratamiento de estos conceptos en la solución de problemas de este tipo, posibilita la formación de una visión global inicial de las habilidades matemáticas para calcular longitudes de segmentos, arcos y amplitudes de ángulos en situaciones dadas.
Los ángulos que intervienen en una circunferencia es el punto de unión entre las figuras geométricas y el circulo, recordando que los triángulos (figura central de la geometría) contiene dos puntos centrales que implican una circunferencia, ahora bien se pueden podemos clasificarlos en 5, los cuales tienen características propias y formula para calcular su arco o bien su angulo, que están relacionados, y estos ángulos son los siguientes:
Ángulo central: Es el ángulo que tiene su vértice en el centro de la circunferencia, es decir, un ángulo determinado por dos semirrectas que tienen el origen en el centro, y por tanto son radios de la circunferencia. Los puntos correspondientes al círculo abarcados por el ángulo central se llaman sector circular correspondiente a dicho ángulo.
Diremos que dos ángulos son equivalentes cuando sus ángulos centrales correspondientes sean iguales.

Característica: La medida del arco AB es la del ángulo central AOB.
Arco AB = Angulo AOB
Ángulo inscrito: Es el ángulo cuyo vértice se encuentra en un punto cualquiera de la circunferencia. Además los lados de un ángulo inscrito son secantes a la circunferencia. El valor del ángulo central es la mitad del ángulo inscrito que abarca el mismo arco.
Si el ángulo central es un ángulo de 180º, entonces el ángulo inscrito es un ángulo de 90º, es decir, un ángulo recto.

Característica: El ángulo inscrito mide la mitad que el arco que comprende.
Ángulo semiinscrito: Es el ángulo cuyo vértice es un punto de la circunferencia y uno de sus lados es tangente a la circunferencia mientras que el otro es secante a ella. El valor de un ángulo semiinscrito es igual al del ángulo inscrito que abarca.

Característica: vale la mitad que el ángulo del centro.
Ángulo exterior: Es el ángulo que tiene su vértice fuera de la circunferencia, es decir que la distancia del vértice al centro es mayor que el radio de la circunferencia; y sus lados son secantes a la circunferencia. El valor de un ángulo exterior es la semidiferencia de los arcos que abarca.

Caracteristica: La medida del ángulo exterior es la semidiferencia de los arcos que abarca.
Ángulo interior: Es el ángulo cuyo vértice está en la parte interior de la circunferencia, es decir, que la distancia del vértice al centro de la circunferencia es menor que el radio. El valor de un ángulo interior es igual a la semisuma de los ángulos que comprenden él mismo y su opuesto.
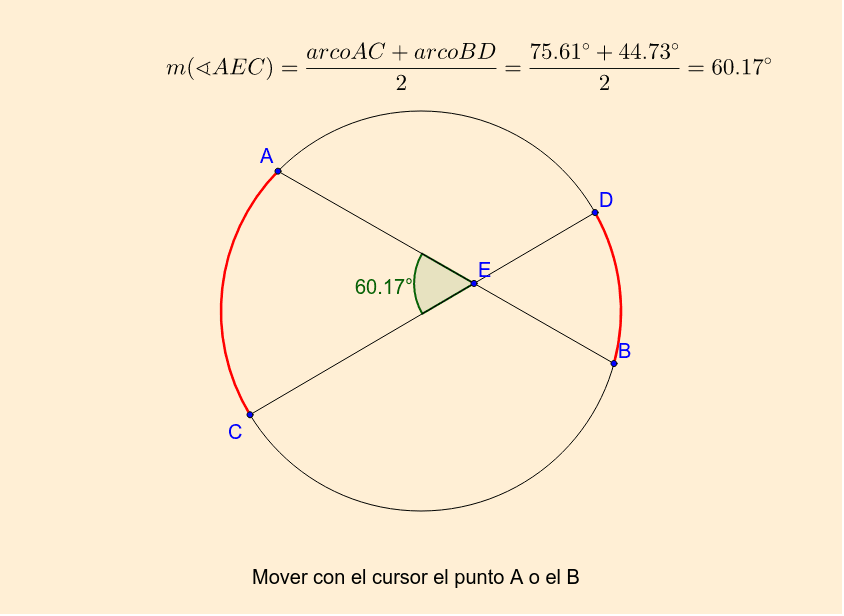
Característica; La medida del ángulo interior es la semisuma de los arcos que comprenden él y su opuesto.
En esta parte te presentaremos algunos ejercicios:
1.- Calcular : “x”

Respuesta: 70, ya que el angulo inscrito es la mitad de un angulo central.
Ahora: ANALIZAR LOS VÍDEOS EN DONDE SE EXPLICA COMO CALCULAR LA APRTURA DEL ANGULO, PERO QUE ES IMPORTANTE PODER IDENTIFICAR DE QUE ANGULO SE TRATA.
No hay comentarios:
Publicar un comentario